因为我们在“重新造轮子”，要从头开始写，没有其他任何函数给我们用，甚至连画线的函数都要自己写。
由于图像是点阵的，我们只能画点，需要用离散的点模拟出线，比如下面这个例子

那么我们应该怎么去画这样的线段呢？
我们知道，两点确定一条直线，表示一条线段的最好方式就是给出2个端点。设2个端点坐标为$(x_a,y_a)$、$(x_b,y_b)$，则我们可以使用两点式表示出改线段所在直线
$$\frac{x-x_a}{x_b-x_a}=\frac{y-y_a}{y_b-y_a}$$
我们可以把该直线写作点斜式：
$$y-y_a=k(x-x_a)$$
其中
$$k=\frac{y_b-y_a}{x_b-x_a}$$
可以写成
$$y=\frac{y_b-y_a}{x_b-x_a}(x-x_a)+y_a$$
因此，我们不妨就遍历所有整数$x_i\in[x_a,x_b]$，找到对应的y，然后四舍五入得到整数$y_i$，那么就可以画出一条线段。
函数实现如下：

void draw_line(int xa, int ya, int xb, int yb, TGAImage &image, TGAColor color)
{
    if(xa > xb) //保证xa<xb
    {
        swap(xa, xb);
        swap(ya, yb);
    }
    //浮点y
    double current_y = ya;
    //步长(也可以理解为斜率)
    double step_y = (yb - ya) / (double)(lenx); 
    for(int xi = xa; xi <= xb; xi++)
    {
        int yi = (current_y + 0.5); //四舍五入
        image.set(xi, yi, color);//画点
        current_y += step_y;
    }
}

我们在main函数里绘制2条线段

int main(int argc, char** argv)
{
    TGAImage image(512, 512, TGAImage::RGB);
    draw_line1(10, 10, 90, 50, image, red);
    draw_line1(10, 10, 90, 170, image, red);
    image.flip_vertically();  //使左下角为原点
    //使用时间作为文件名
    time_t timer;
    time(&timer);
    string com = "./output/" + to_string(timer) + ".tga";
    image.write_tga_file(com.c_str());
    return 0;
}

得到的效果如下图，我们会发现，斜率$k\in[-1,1]$的线段可以很好地画出，但是更陡峭一些的线，如果使用x遍历，那么y每次跳跃超过1，并不连续。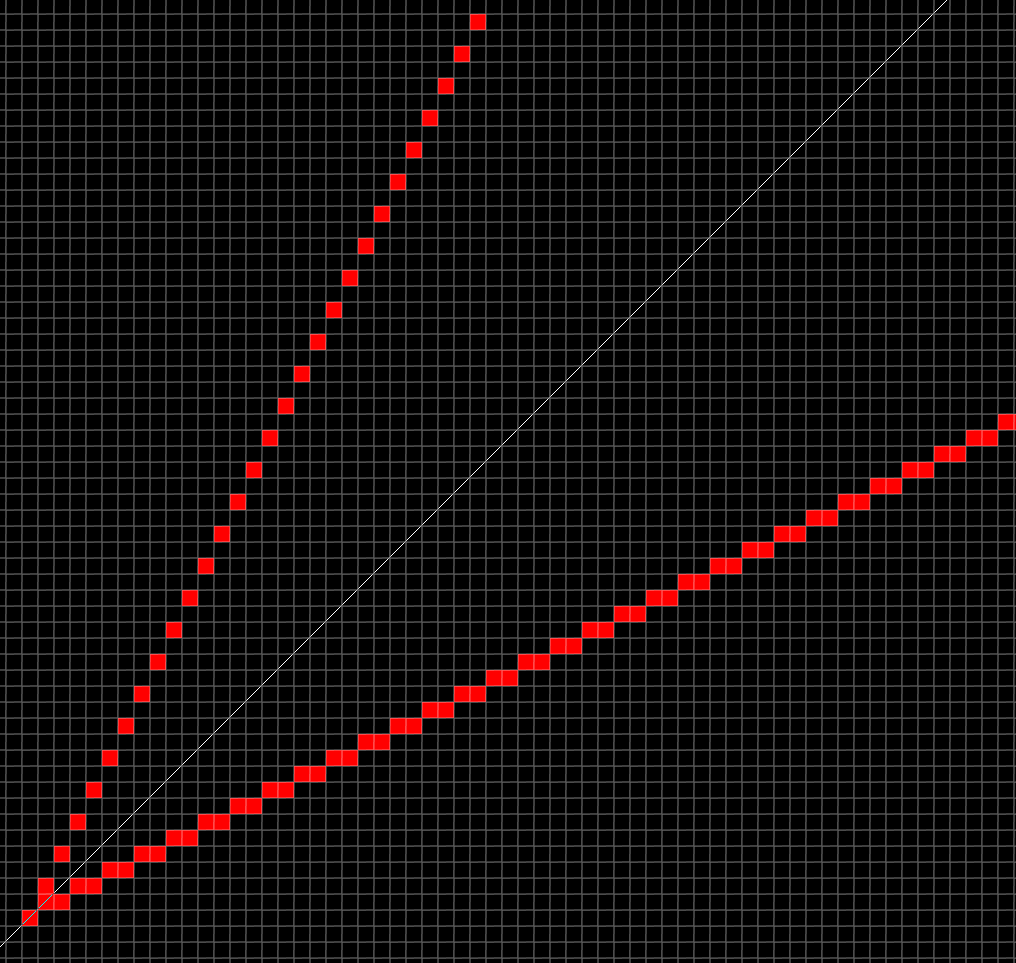

我们考虑优化一下，在$\left|k\right|>1$情况下，我们会发现，我们可以把它看成$k’=\frac{1}{k}$的对称情况。因此，在这种情况下，用y遍历就可以保证线段连续。最终代码如下：

void draw_line(int xa, int ya, int xb, int yb, TGAImage &image, TGAColor color)
{
    int lenx = abs(xa - xb), leny = abs(ya - yb);//在x\y方向上的长度
    if(lenx >= leny) //如果斜率在[-1,1]，就以横坐标遍历
    {
        if(lenx == 0) //如果是一个点
        {
            image.set(xa, ya, color);
            return;
        }
        if(xa > xb) //保证xa<xb
        {
            swap(xa, xb);
            swap(ya, yb);
        }
        double current_y = ya; //浮点的y
        double step_y = (yb - ya) / (double)(lenx); //步长(也可以理解为斜率)
        for(int xi = xa; xi <= xb; xi++)
        {
            int yi = (current_y + 0.5); //四舍五入
            image.set(xi, yi, color);
            current_y += step_y;
        }
    }
    else //斜率绝对值大于1，以纵坐标遍历
    {
        if(ya > yb)
        {
            swap(xa, xb);
            swap(ya, yb);
        }
        double current_x = xa;
        double step_x = (xb - xa) / (double)leny;
        for(int yi = ya; yi <= yb; yi++)
        {
            int xi = (current_x + 0.5);
            image.set(xi, yi, color);
            current_x += step_x;
        }
    }
}
/*补充说明：这段代码可以处理一些极端情况。
当线段起点终点重合，进行了特判，避免了除以lenx(==0)的情况。
当斜率不存在或为0时，并不会出错，因为在这种情况下，会分别进入对应横向的遍历方式，避免了除以lenx/leny(==0)的情况。
*/

这样就可以连续地画出所有的线啦！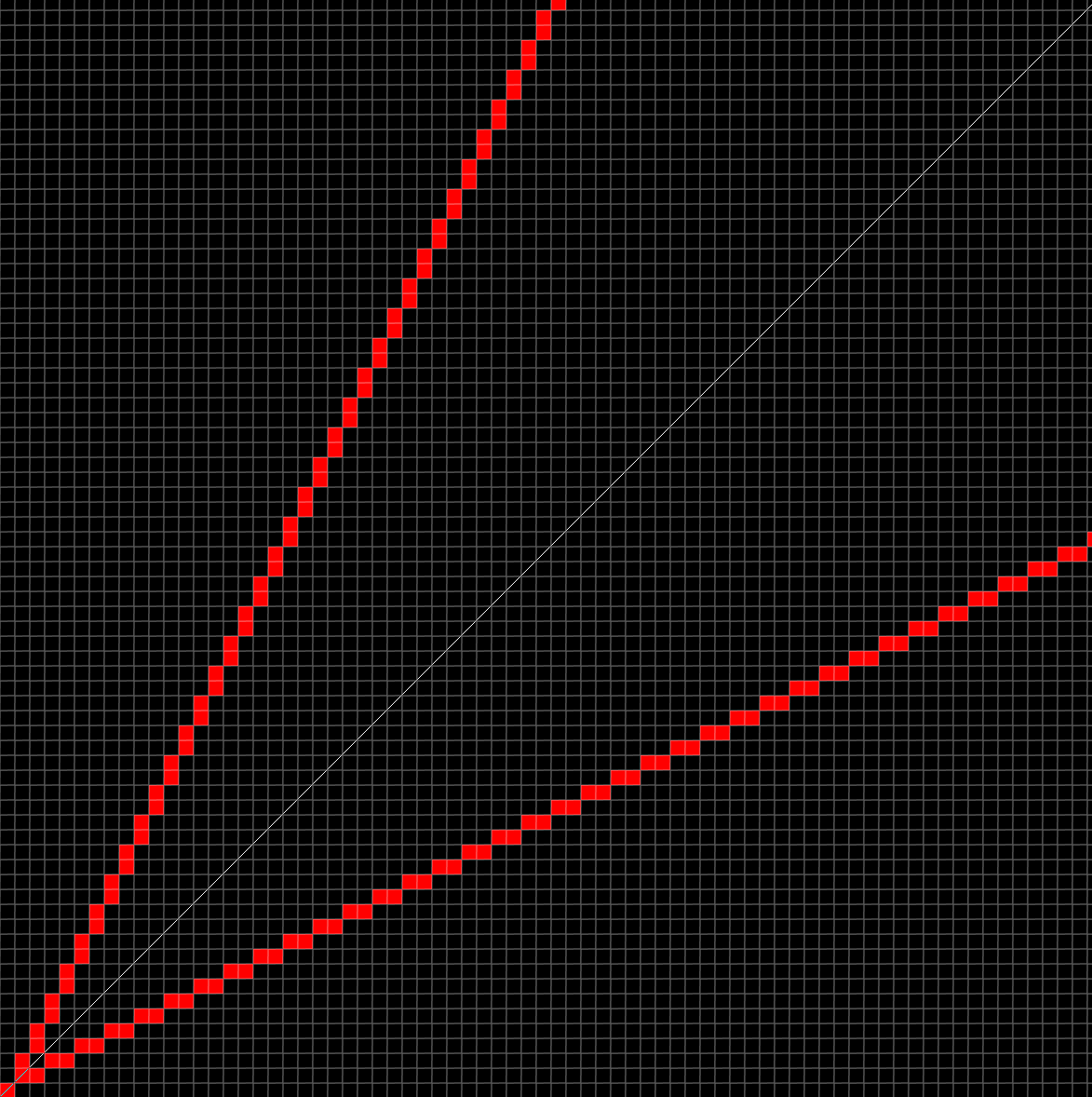

最后，我对该画线函数进行了性能测试。在512×512的图片上，随机绘制 $10^5$条直线，用时平均约0.27秒，可以看出效率还可以接受。

/*
测试 draw_line() 速度
随机绘制100000条线 
三次分别用时 0.280 s 0.267 s 0.275 s
*/
for(int i = 0; i <= 100000; i++)
{
    draw_line(rand() % 512, rand() % 512, rand() % 512, rand() % 512, image, red);
}

到此为止，我们的渲染器终于可以画线啦，是不是很激动[doge]。开个玩笑，我们忙活了这么久，居然才实现了这么一个简单的功能，后面还有很长的路要走。